A geodesic sphere approximately one-half mile in diameter would float away like a soap bubble if the air inside it were one degree warmer than the air outside.
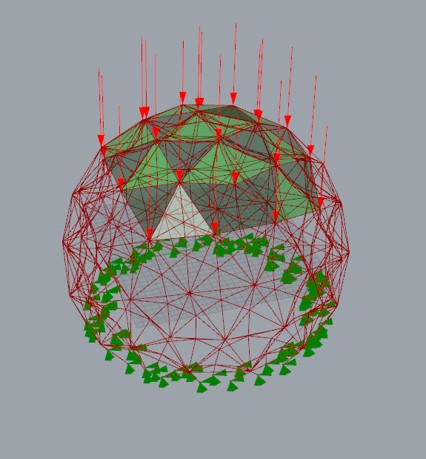
For this university project, I wanted to test if Hugh Kenner's claim was accurate. The tought behind this is that a geodesic shape is so structurally efficient (and therefore lightweight) that the buoyancy force (the same force that makes a hot air balloon fly) is enough to make it float. You can visualise below the type of geodesic sphere that I modelled in Grasshopper. I decided to model a truss structure based on Buckminster Fuller's Montreal Biosphere. Each colour represents a distinct member length (notice the patterns of a geodesic structure).
To make things more interesting, I assumed different design conditions:
- Instead of sphere, I will cary the experiment on a grounded geodesic dome, in shape and proportions similar to the Montreal Biosphere
- The dome is located in Antartica where the outisde temperature is -20C and the inside temperature is +15C
- Since it is located in Antartica, I have to design the dome for wind and snow load
- The buckling of members are ignored. We'll be using CHS so theroretically the I value can get pretty high for a constant cross sectional area
- High strength steel is used: $$ {f_y=450MPA} $$
Methodology
There are three governing parameters to the structural performance of the geodesic dome:- The frequency of the geodesic subdivison i.e. how many triangles the dome is composed of.
- The sphere radius (which Hugh Kenner says makes the dome float at a quarter mile radius).
- The truss depth which is set at 10% of the radiusand thus treated as a constant.
For a range of those parameters, I will be recording the buoyancy ratio to see if it drops below 1 at any point.
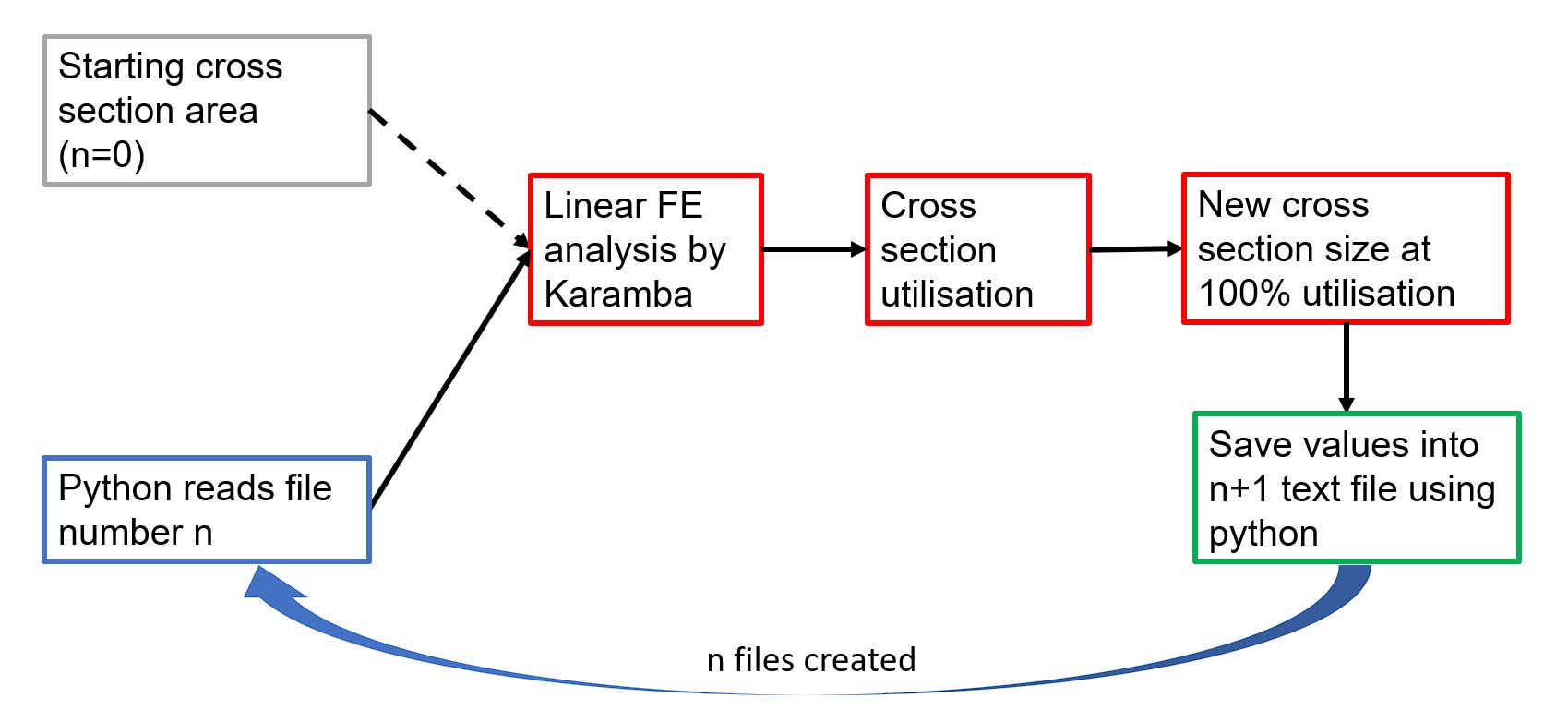
Finite Element Analysis
The tricky part of this study is sizing the members appropriately to resist the self-weight of the structure, the wind and the snow load. Luckily on Grasshopper this can be automated and calculated for a range of dome size using the FEA package Karamba. Snow Load is applied to any surface at an angle less than 45° to the horizontal:
Results
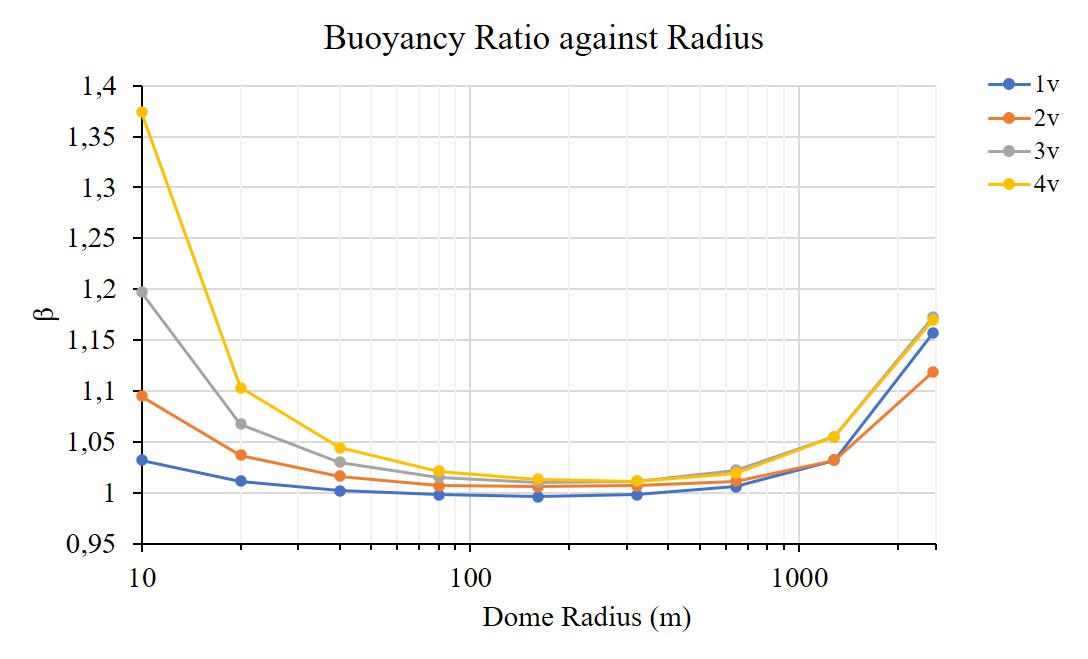
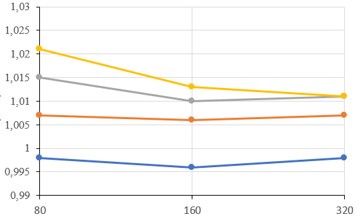
I plotted the results with the dome radius in the x axis (logarithmic) and the buoyancy ratio in the y axis (structure floats if less than 1). There are four lines, one for each level of subdivison (the higher subdivisions, the more the shape converges toward a sphere). The results show that the optimal dome radius for any level of subdivision is 160 meter radius and that for a subdivision of 1, the buoyancy ratio is just under 1, meaning the structure would theoretically float. What is suprising from the results is the shape of the curve. I expected the curve to be negatively correlated to the dome radius as the buoyancy force is proportional to the volume of the sphere (which exponentially increases with the dome radius). It is also suprising that, the lower the frequency of subdivision, the higher the efficiency of the structure. This may be due to its simplified shape which accomodates less snow and wind load. In reality, for a low frequency of subdivison, members are longer and thus more prone to buckling. Designing for buckling would have increased the member sizes and thus the weight of the structure.